目录
经典算法思想
分治法(Divide and Conquer)
分治法(Divide and Conquer,也称为“分而治之法”)是一种很重要的算法,我们可以应用分治法来逐一拆解复杂的问题,核心思想就是将一个难以直接解决的大问题依照相同的概念分割成两个或更多的子问题,以便名个击破。
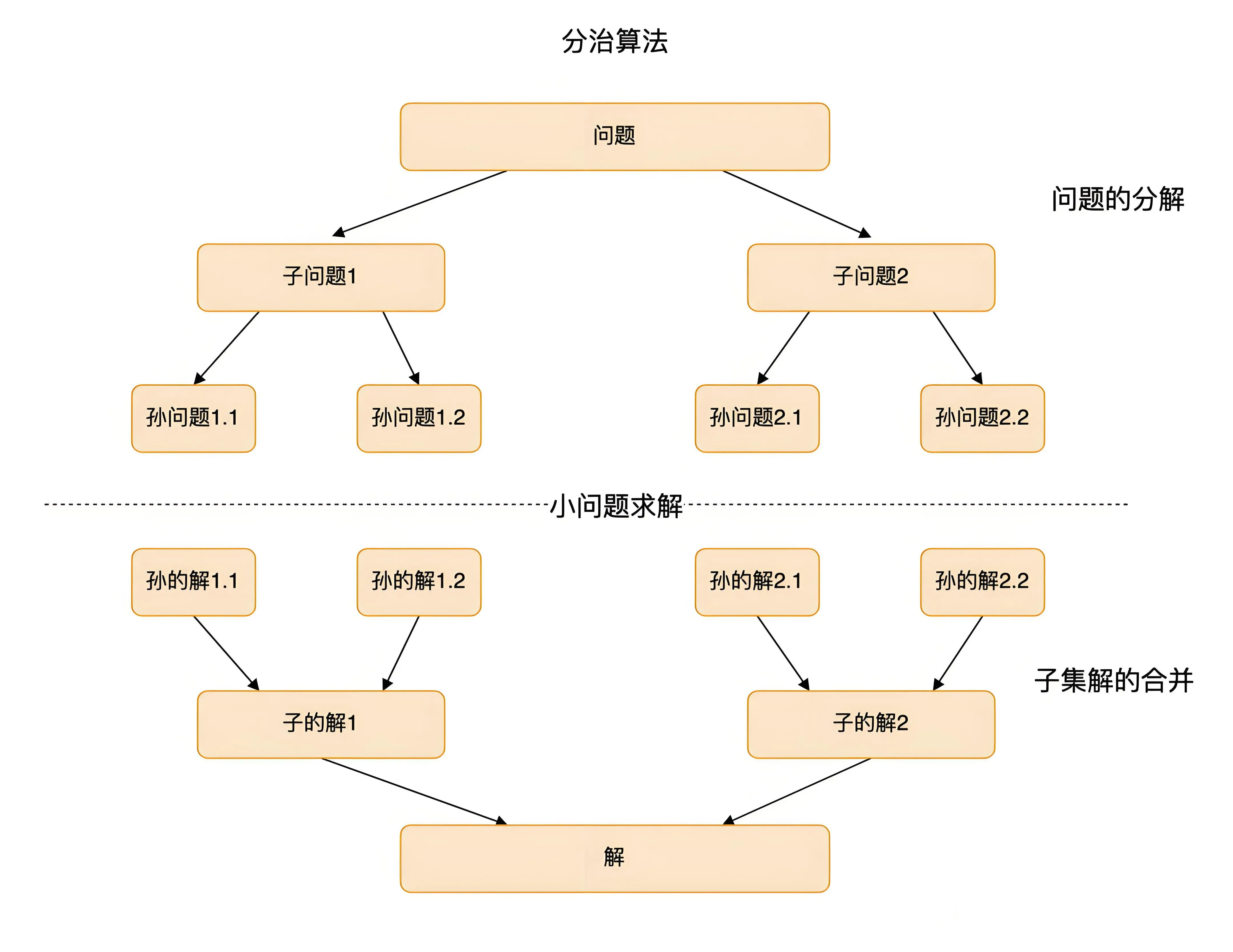
其实任何一个可以用程序求解的问题所需的计算时间都与其规模与复杂度有关,问题的规模越小,越容易直接求解,因此可以不断分解问题,使子问题规模不断缩小,让这些子问题简单到可以直接解决,再将各子问题的解合并,最后得到原问题的解答。
特点与应用
- 子问题相互独立
- 递归实现
- 归并排序:将数组拆分为两半,递归排序后合并有序子数组。
- 快速排序:通过基准值分割数组,递归处理左右分区
代码实现(归并排序)
javapublic class MergeSort {
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
mergeSort(arr, left, mid); // 分解左半部分
mergeSort(arr, mid + 1, right); // 分解右半部分
merge(arr, left, mid, right); // 合并有序子数组
}
}
private static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
temp[k++] = (arr[i] <= arr[j]) ? arr[i++] : arr[j++];
}
while (i <= mid) temp[k++] = arr[i++];
while (j <= right) temp[k++] = arr[j++];
System.arraycopy(temp, 0, arr, left, temp.length);
}
public static void main(String[] args) {
int[] arr = {5, 3, 8, 4, 2};
mergeSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr)); // 输出[2, 3, 4, 5, 8]
}
}
代码解读:
分解:递归将数组分为左右两半
合并:将两个有序子数组合并为一个有序数组
递归法(Recursion)
递归是一种很特殊的算法,分治法和递归法很像一对孪生兄弟,都是将一个复杂的算法问题进行分解,让规模越来越小,最终使子问题容易求解。只不过递归法通过函数调用自身解决问题,需定义基线条件和递归条件。
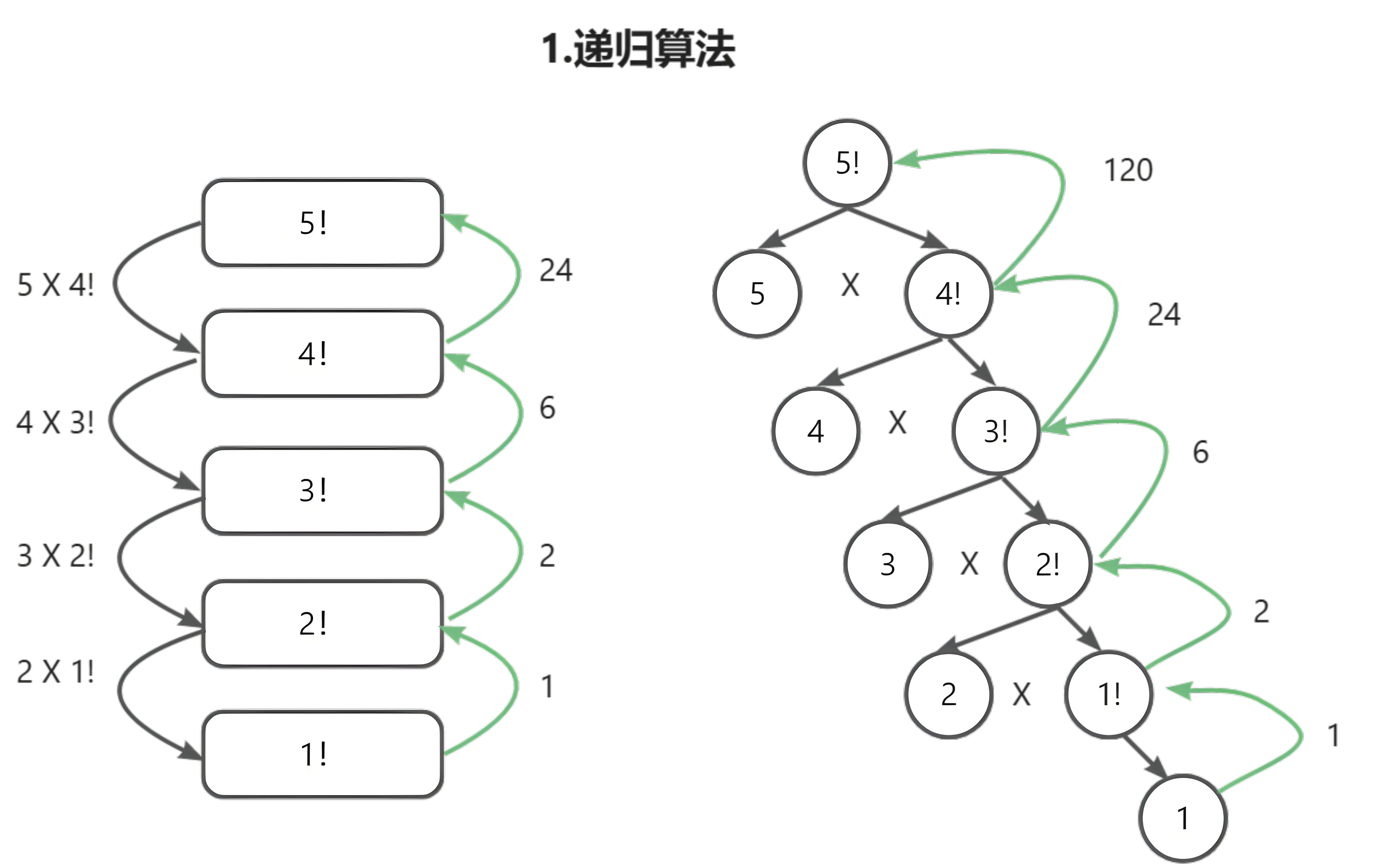
特点与应用
- 代码简洁
- 经典应用:树遍历、汉诺塔
汉诺塔问题
给定三根柱子,记为 A,B,C,其中 A 柱子上有 n 个盘子,从上到下编号为 0 到 n−1 ,且上面的盘子一定比下面的盘子小。问:将 A 柱上的盘子经由 B 柱移动到 C 柱最少需要多少次?打印出每个步骤
移动时应注意:
- 一次只能移动一个盘子
- 大的盘子不能压在小盘子上
思路
先从简单的三个盘子试试,可以先不看答案自己画一画,挺好玩的,注意规则噢
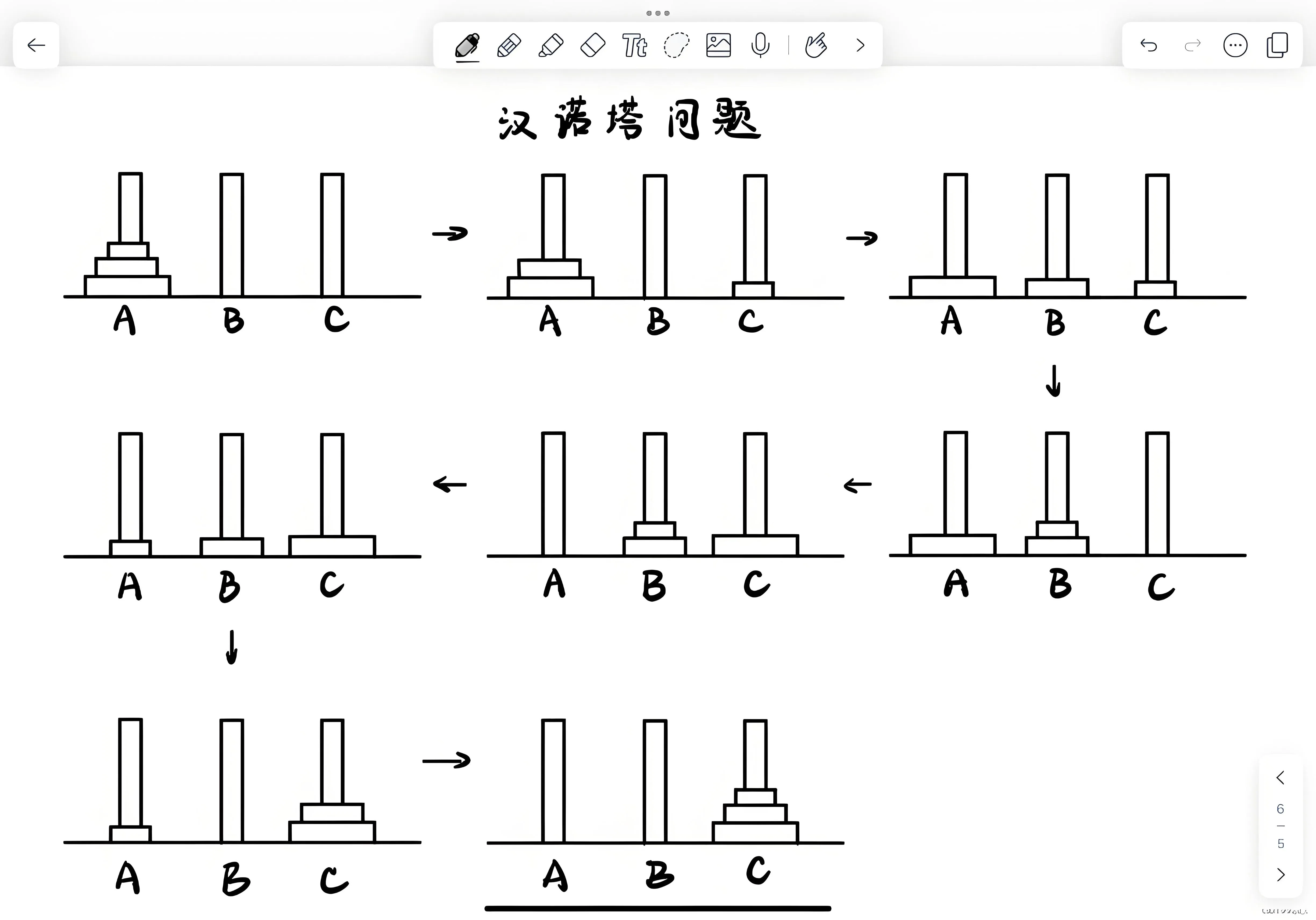
n个盘子从A柱到C柱最少移动次数

代码实现
javapublic class HanoiTower {
public static void move(int n, char from, char to, char aux) {
if (n == 1) {
System.out.println("移动盘子1从" + from + "到" + to);
return;
}
move(n - 1, from, aux, to);
System.out.println("移动盘子" + n + "从" + from + "到" + to);
move(n - 1, aux, to, from);
}
public static void main(String[] args) {
move(3, 'A', 'C', 'B'); // 3层汉诺塔解法
}
}
代码解读
将n个盘子分解为移动n-1个盘子的子问题
时间复杂度:O(2ⁿ)
动态规划(Dynamic Programming, DP)
通过记录子问题的解避免重复计算,适用于有重叠子问题和最优子结构的问题。
动态规划法(Dynamic Programming Algorithm,DPA)类似于分治法,核心思想是如果一个问题的答案与子问题相关,就将大问题拆解成各个小问题,与分治法最大的不同是可以让每一个子问题的答案被存储起来,以供下次求解时直接取用。这样的做法不但可以减少再次计算的时间,而且可以将这些解组合成大问题的解,故而使用动态规划可以解决重复计算的问题。
动态规划法是分治法的延伸。当用递归法分割出来的问题“一而再,再而三”出现时,就可以运用记忆(Memorization)法来存储这些问题。与分治法不同的地方在于,动态规划法增加了记忆机制的使用,将处理过的子问题的答案记录下来,避免重复计算。
特点与应用
- 自底向上或自顶向下(记忆化搜索)
- 时间复杂度优化显著
- 最短路径问题(Floyd-Warshall算法)
- 斐波那契数列
- 背包问题
- 最长公共子序列
- 最长公共子串
- 矩阵最大值(和以及积)
斐波那契数列
斐波那契数列是指这样一个数列:0,1,1,2,3,5,8,13,21,34,55,89……这个数列从第3项开始 ,每一项都等于前两项之和。
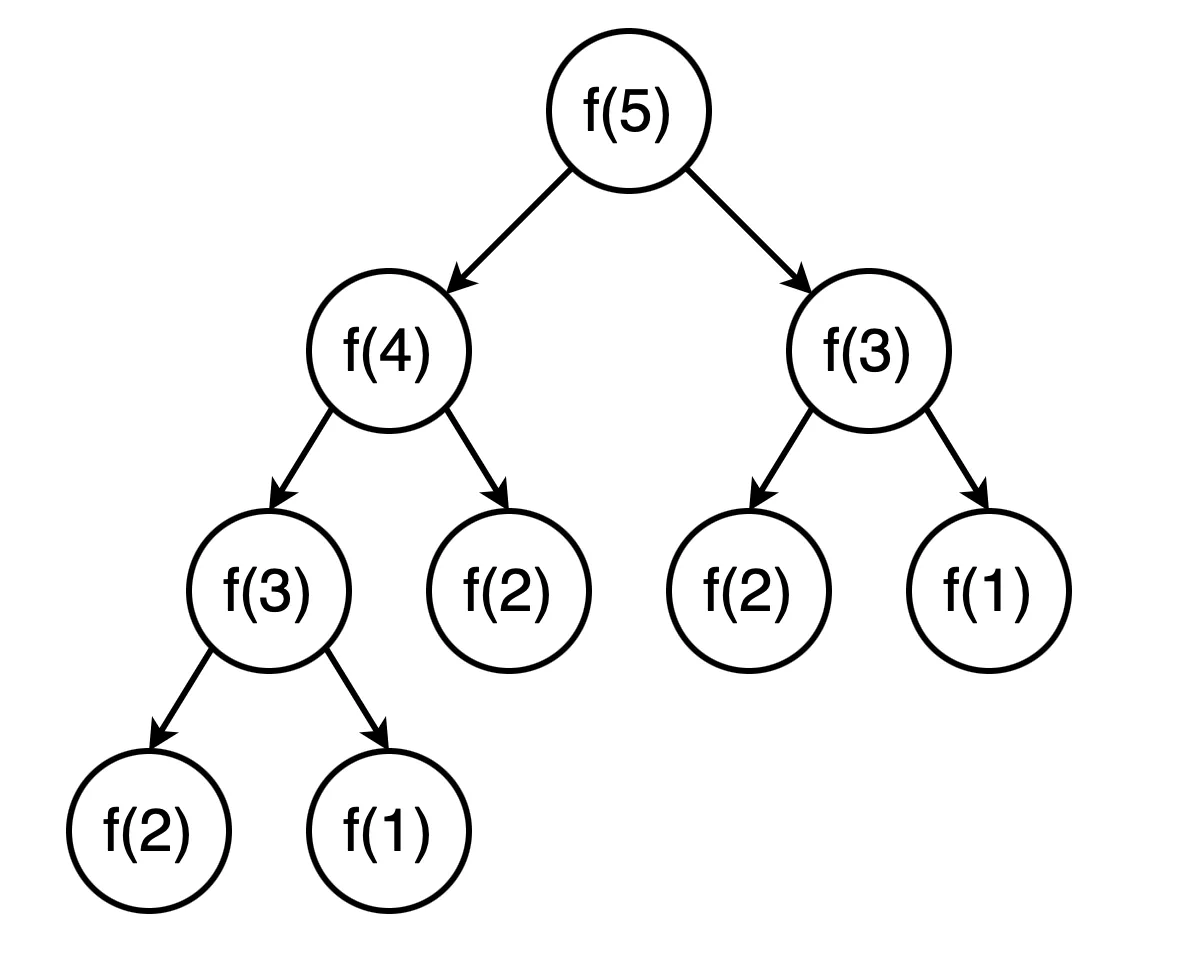
对于斐波那契数列采用的是动态规划法,那么已计算过的数据就不必重复计算了,也不会再往下递归,这样可以提高性能。
代码实现
javapublic class Fibonacci {
// 动态规划实现
public static int fibDP(int n) {
if (n <= 1) return n;
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
public static void main(String[] args) {
System.out.println(fibDP(10)); // 输出55
}
}
代码解读:
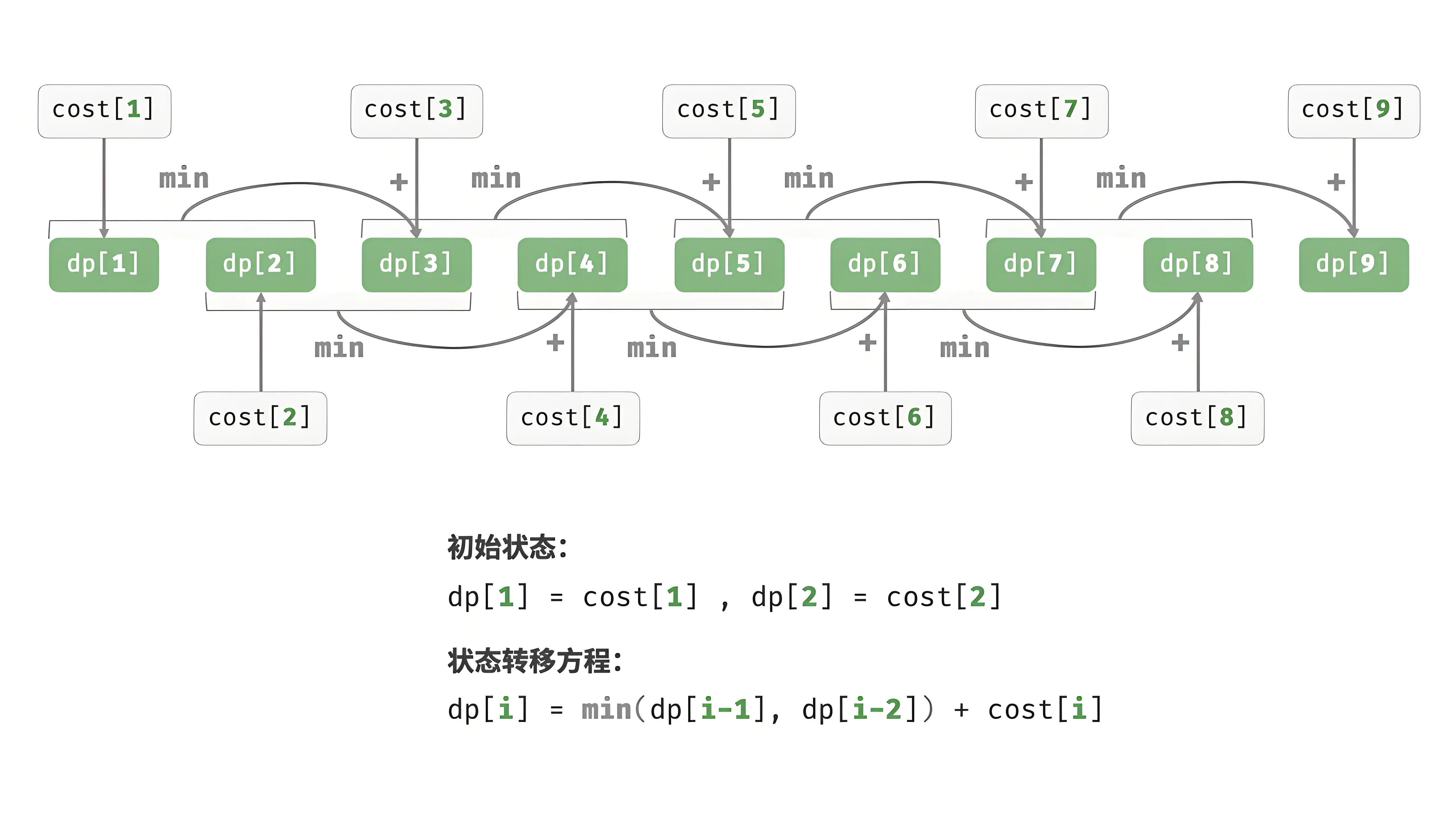
使用数组 dp 存储中间结果
递推公式:dp[i] = dp[i-1] + dp[i-2]
枚举法(Brute Force)
枚举法(又称为穷举法),是我们在日常工作中使用最多的一种算法,核心思想是列举所有的可能。根据问题的要求,逐一列举问题的解答,或者为了便于解决问题把问题分为不重复、不遗漏的有限种情况,逐一列举各种情况,并加以解决,最终达到解决整个问题的目的。像枚举法这种分析问题、解决问题的方法,得到的结果总是正确的,缺点是速度太慢。
特点与应用
- 实现简单
- 时间复杂度:O(n)
- 适合小规模的问题
- 密码破解:尝试所有可能的字符组合
代码实现
使用穷举法来实现以下题目
今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
javapublic class Permutations {
public static void enumeratingAlgorithm() {
int head = 35, foot = 94;
int j;
for (int i = 0; i <= 35; i++) {
// i代表鸡的数量
j = head - i;
// j代表兔子的数量
if (i * 2 + j * 4 == foot) {
System.out.printf("鸡的个数为[ %d ]只,兔子的个数为[ %d ]只。", i, j);
return;
}
}
System.out.println("此题无解!你家鸡和兔子有三只脚的吧?");
}
}
代码解读:
通过题目可以知道,鸡和兔的总数量为0-35只(每个动物都是一个脑袋,这就不用说了吧),我们可以假设鸡为0,兔子为35,用鸡的个数2+兔子的个数4就可以得到总的脚的数量,如果等于94,那么便是答案,如果不等,则鸡的数量+1,兔子数量-1,依次类推,穷举所有情况直到得到答案
回溯法(Backtracking)
回溯法(Backtracking)也是枚举法的一种,对于某些问题而言,回溯法是一种可以找出所有(或一部分)解的一般性算法,同时避免枚举不正确的数值。一旦发现不正确的数值,就不再递归到下一层,而是回溯到上一层,以节省时间,是一种走不通就退回再走的方式。它的特点主要是在搜索过程中寻找问题的解,当发现不满足求解条件时就回湖(返回),尝试别的路径,避免无效搜

特点
- 递归实现
- 时间复杂度高(指数级)
- 数独求解
- 组合数生成
- A*寻路算法(了解)
- 地图着色算法
- N 皇后问题
- 最优加工顺序
- 旅行商问题
回溯法可以应用于以下类型的问题:
- 排列和组合问题:例如求解全排列、子集合等问题,回溯法可以系统地生成所有可能的组合并逐一验证。
- 决策问题:如八皇后问题、数独填充、图的着色问题等,这些问题需要在多个选择中找到符合特定约束的解。
- 优化问题:如旅行商问题(TSP)和其他需要找到最优解的问题,回溯法可以遍历所有可能的解,找到成本最低或收益最高的解。
- 分割问题:例如分割等和子集、装箱问题等,需要将集合分割成满足特定条件的多个子集。
N皇后问题
八皇后问题,是一个古老而著名的问题.该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法?

将8皇后问题推演一下,就可以得到我们的N皇后问题了。
N皇后问题是一个经典的问题,在一个N*N的棋盘上放置N个皇后,使其不能互相攻击。(同一行、同一列、同一斜线上的皇后都会自动攻击)那么问,有多少种摆法?
代码解读:
javapublic class NQueens {
private static List<List<String>> result = new ArrayList<>();
public static List<List<String>> solveNQueens(int n) {
char[][] board = new char[n][n];
for (char[] row : board) Arrays.fill(row, '.');
backtrack(board, 0);
return result;
}
private static void backtrack(char[][] board, int row) {
if (row == board.length) {
result.add(convertBoard(board));
return;
}
for (int col = 0; col < board.length; col++) {
if (isValid(board, row, col)) {
board[row][col] = 'Q';
backtrack(board, row + 1);
board[row][col] = '.'; // 回溯
}
}
}
private static boolean isValid(char[][] board, int row, int col) {
// 检查列、左上对角线、右上对角线
for (int i = 0; i < row; i++) {
if (board[i][col] == 'Q') return false;
int left = col - (row - i), right = col + (row - i);
if (left >= 0 && board[i][left] == 'Q') return false;
if (right < board.length && board[i][right] == 'Q') return false;
}
return true;
}
private static List<String> convertBoard(char[][] board) {
List<String> res = new ArrayList<>();
for (char[] row : board) res.add(new String(row));
return res;
}
public static void main(String[] args) {
System.out.println(solveNQueens(4).size()); // 输出2(4皇后有2种解法)
}
}
代码解读:
逐行放置皇后,检查冲突
回溯时重置棋盘状态(board[row][col] = '.')
贪心法(Greedy Algorithm)
贪心算法(greedy algorithm,又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。
思路
贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行,根据某个优化测度,每一步都要确保能获得局部最优解。每一步只考虑一个数据,其选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时, 就不把该数据添加到部分解中,直到把所有数据枚举完,或者不能再添加算法停止。
贪心算法的核心问题是选择能产生问题最优解的最优度量标准,即具体的贪心策略。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择。
题解思路可分为3个步骤
- 将问题分解为多个子问题。
- 选择合适的贪心策略,得到每一个子问题的局部最优解。
- 将子问题的局部最优解合并成原问题的最优解。
贪心算法存在的问题
贪心算法是把求解的问题分成若干个子问题求最优解,不能保证 最终解是最佳的。
因为贪心算法总是从局部出发,并没从整体考虑,贪心算法容易过早做出决定,所以只能求出满足某些约東条件的解,而有时在某些问题上还是可以得到最优解的。
解题策略
要确定一个问题是否适合用贪心算法求解,必须证明每一步所作的贪心选择最终导致问题的整体最优解,使用贪心策略解题需要考虑以下两个问题:
- 该问题是否适合使用贪心策略求解,也就是该问题是否具有贪心选择性质
- 制定贪心策略,以达到问题的最优解或较优解
证明的大致过程
首先考察问题的一个整体最优解,并证明可修改这个最优解,使其以贪心选择开始,做了贪心选择后,原问题简化为规模更小的类似子问题。然后用数学归纳法证明通过每一步做贪心选择,最终可得到问题的整体最优解。
经典应用
贪心策略的经典算法
分数背包问题
给定 n 个物品,每个物品都有重量 w[i] 和价值 v[i],同时有一个容量为 C 的背包。与 0-1 背包问题不同的是,在分数背包问题中,物品可以分割成任意比例放入背包,目标是在背包容量限制内选择物品放入背包,使得背包中物品的总价值最大。
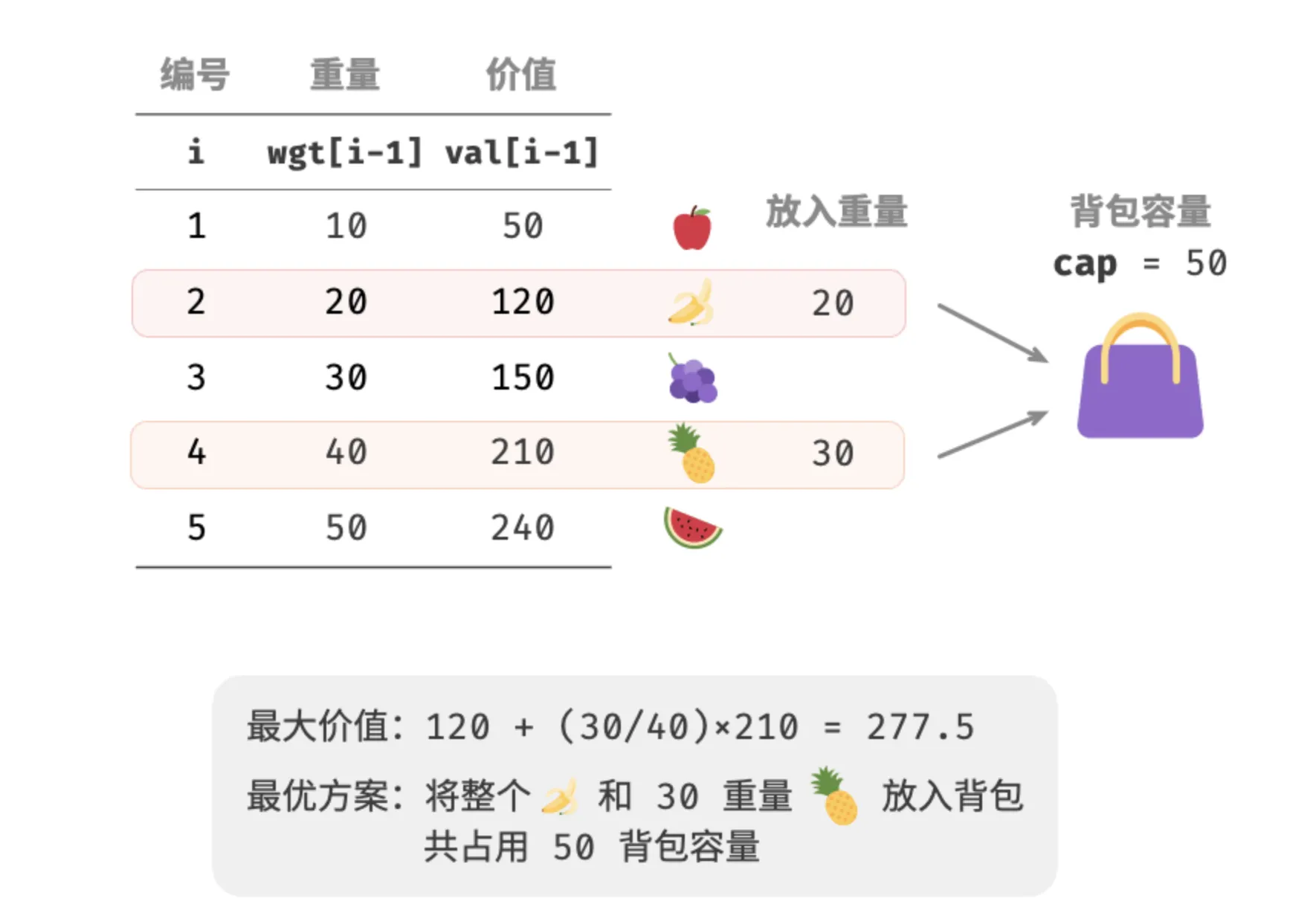
贪心策略确定
最大化背包内物品总价值,本质上是最大化单位重量下的物品价值。由此便可推理出贪心策略。
- 将物品按照单位价值从高到低进行排序。
- 遍历所有物品,每轮贪心地选择单位价值最高的物品。
- 若剩余背包容量不足,则使用当前物品的一部分填满背包。

代码实现
建立了一个物品类 Item ,以便将物品按照单位价值进行排序。循环进行贪心选择,当背包已满时跳出并返回解:
java/* 物品 */
class Item {
int w; // 物品重量
int v; // 物品价值
public Item(int w, int v) {
this.w = w;
this.v = v;
}
}
/* 分数背包:贪心 */
double fractionalKnapsack(int[] wgt, int[] val, int cap) {
// 创建物品列表,包含两个属性:重量、价值
Item[] items = new Item[wgt.length];
for (int i = 0; i < wgt.length; i++) {
items[i] = new Item(wgt[i], val[i]);
}
// 按照单位价值 item.v / item.w 从高到低进行排序
Arrays.sort(items, Comparator.comparingDouble(item -> -((double) item.v / item.w)));
// 循环贪心选择
double res = 0;
for (Item item : items) {
if (item.w <= cap) {
// 若剩余容量充足,则将当前物品整个装进背包
res += item.v;
cap -= item.w;
} else {
// 若剩余容量不足,则将当前物品的一部分装进背包
res += (double) item.v / item.w * cap;
// 已无剩余容量,因此跳出循环
break;
}
}
return res;
}
内置排序算法的时间复杂度通常为O(logn) ,空间复杂度通常为 O(logn) 或 O(n),取决于编程语言的具体实现。除排序之外,在最差情况下,需要遍历整个物品列表,因此时间复杂度为O(n),其中n为物品数量。由于初始化了一个 Item 对象列表,因此空间复杂度为 O(n)。
正确性证明
采用反证法。假设物品 x 是单位价值最高的物品,使用某算法求得最大价值为 res ,但该解中不包含物品 x。
现在从背包中拿出单位重量的任意物品,并替换为单位重量的物品x。由于物品x的单位价值最高,因此替换后的总价值一定大于 res 。这与 res 是最优解矛盾,说明最优解中必须包含物品x。
对于该解中的其他物品,我们也可以构建出上述矛盾。总而言之,单位价值更大的物品总是更优选择,这说明贪心策略是有效的。
将物品重量和物品单位价值分别看作一张二维图表的横轴和纵轴,则分数背包问题可转化为“求在有限横轴区间下围成的最大面积”。这个类比可以帮助我们从几何角度理解贪心策略的有效性。
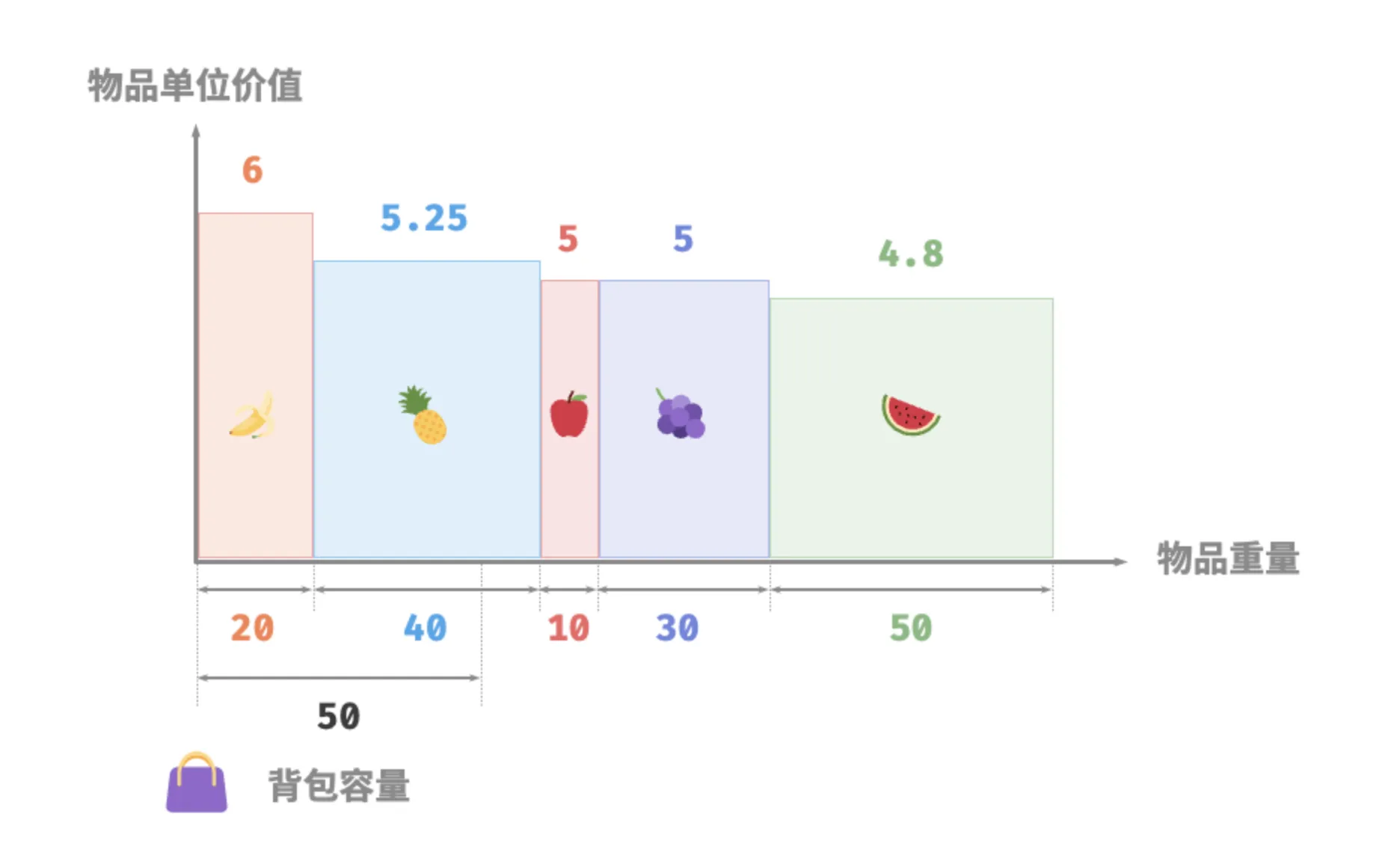
找零问题
给定一个总金额和一系列不同面额的零钱,如何以最少的零钱数量来支付这个金额。在找零问题中,贪心算法的核心思想是每一步尽可能使用面值最大的零钱,从而减少使用的零钱数量。
贪心策略确定
将原问题分解为一系列子问题,每个子问题对应一个具体的找零操作。
- 贪心选择:对每个子问题求解时,选择当前看起来“最优”的解法,即尽可能使用面值最大的零钱。
- 合并解:累计局部最优解形成全局解,最终得到最少的零钱数量。
代码实现
javapublic class CoinChange {
public static int minCoins(int[] coins, int amount) {
Arrays.sort(coins); // 需降序排序
int count = 0, index = coins.length - 1;
while (amount > 0 && index >= 0) {
if (coins[index] <= amount) {
int num = amount / coins[index];
count += num;
amount -= num * coins[index];
}
index--;
}
return (amount == 0) ? count : -1;
}
public static void main(String[] args) {
int[] coins = {1, 5, 10, 25}; // 美分硬币
System.out.println(minCoins(coins, 63)); // 输出6(25+25+10+1+1+1)
}
}
正确性证明
通过数学归纳或替换论证验证算法的正确性,尽管贪心策略不一定总是正确的,但在许多情况下能够提供足够好的解决方案。
总结
掌握这些算法思想可覆盖90%的编程问题,实际应用中需根据问题特点灵活组合使用。
| 算法思想 | 适用场景 | 时间复杂度 |
|---|---|---|
| 分治法 | 大规模问题分解 | O(n log n) |
| 递归法 | 树形结构问题 | 取决于问题规模 |
| 动态规划 | 重叠子问题优化 | O(n²) ~ O(n³) |
| 枚举法 | 小规模暴力求解 | O(2ⁿ) ~ O(n!) |
| 回溯法 | 组合优化问题 | O(n!) |
| 贪心法 | 局部最优解场景 | O(n) ~ O(n log n) |


本文作者:柳始恭
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
